ניתוח מפורט של מעגל סדרת RC
2024-05-08
20622
מעגל סדרת RC, המורכב מנגד וקבל, משמש כמרכיב בסיסי בעיצובים של מערכת אלקטרונית בסיסית ומתקדמת כאחד.זה עוזר להבין עקרונות מפתח כמו תגובת תדרים, משמרת פאזות וסינון אותות, הממלאים תפקיד משמעותי בעיצוב המעגלים ועיבוד האות.חקר זה מכסה יסודות תיאורטיים ומתרחב ליישומים מעשיים באמצעות ניסויים והדמיות.על ידי הרכבת פיזית של המעגל או הדוגמנות שלו באופן דיגיטלי, הלומדים יכולים לתפוס חזותית את תהליך הטעינה ואת ההשפעות של יוני רכיב V ariat, מה שהופך מושגים מורכבים לנגישים יותר ובלתי נשכחים.
קָטָלוֹג

איור 1: מתחי יציאה שונים של מעגלי RC
מבוא למעגל RC
מעגל RC, קיצור של מעגל קיבול התנגדות, הוא בסיסי באלקטרוניקה לתמרון אותות דרך נגדים וקבלים.מעגלים אלה ידועים במיוחד ביכולתם להעביר שלבים ולסנן אותות, תוך שימוש בסידורים פשוטים של רכיבים אלה.מעגל RC בסיסי, המכונה לעתים קרובות מעגל RC מסדר ראשון, כולל בדרך כלל רק נגדי אחד וקבל אחד.
במערך טיפוסי מתח הכניסה מוחל על סידור הסדרה של נגדי וקבל.ניתן לצייר את הפלט על פני הנגד או הקבל, כאשר כל אחד מהם נותן תגובות שונות לתדרי איתות בגלל המאפיינים הייחודיים של הקבל.צדדיות זו מאפשרת למעגלי RC לבצע מגוון תפקידים במכשירים אלקטרוניים, כגון אותות צימוד וסינון או אפילו המרת צורות גל כאשר הן נתונות למתח צעד.
ניתן להגדיר את מעגל ה- RC בכמה דרכים-סדרות, מקבילות או שילוב של שניהם, המכונה סדרה מקבילה.כל תצורה משפיעה על תדרי האות באופן שונה: חיבורי סדרה נוטים להחליש תדרים נמוכים, ואילו חיבורים מקבילים משמשים לניצול תדרים גבוהים יותר.הבדל זה נובע בעיקר מהדרך בה נגדים וקבלים מקיימים אינטראקציה עם המעגל;נגדים מתנגדים ישירות לזרם בזמן שקבלים מאחסנים ומשחררים אותו, ומשפיעים על אופן ההגבה של המעגל לתדרים שונים.
בניגוד למעגלים הכוללים משרנים, כמו מעגלי LC, מעגלי RC פשוטים אינם יכולים להדהד מכיוון שנגדים אינם מאחסנים אנרגיה.תכונה זו משפיעה באופן מובהק על אופן השימוש במעגלי RC, ומתמקדים ביכולתם לסינון ולא באחסון אנרגיה או תהודה.כל תצורה משרתת מטרה ספציפית, מה שהופך מעגלי RC לכלים רב -תכליתיים הן במחקר תיאורטי והן ביישום מעשי בעיצוב אלקטרוני.
מעגל סדרת RC
מעגל סדרת RC, המורכב בעיקר מנגד (ר ') וקבל (ג) בסדרה, פועלת על פי עיקרון פשוט.כאשר מתג המעגל סגור, הקבל מתחיל לטעון מהמתח המופעל (V), יוזם זרימת זרם דרך המעגל.כאשר הקבל גובה, הזרם גדל בהדרגה עד שהקבל יגיע לקיבולתו, ובשלב זה הוא מפסיק לקבל מטען, והזרם מתייצב בערכו המרבי, מחושב כ-  ו
ו
 ו
וניתן לתאר את תהליך הטעינה של הקבל באופן מתמטי על ידי המשוואה 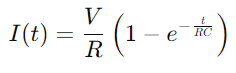 , איפה שאני הנוכחי, V הוא המתח, ר ' היא ההתנגדות, ג הוא הקיבול, t זה הזמן, ו ה הוא בסיס הלוגריתם הטבעי.נוסחה זו משקפת כיצד הזרם משתנה לאורך זמן כאשר הקבל מטען, כאשר תוצר ערכי ההתנגדות והקיבול (RC) מגדירים את קבוע הזמן של המעגל, המעיד על המהירות בה הקבל מטען.
, איפה שאני הנוכחי, V הוא המתח, ר ' היא ההתנגדות, ג הוא הקיבול, t זה הזמן, ו ה הוא בסיס הלוגריתם הטבעי.נוסחה זו משקפת כיצד הזרם משתנה לאורך זמן כאשר הקבל מטען, כאשר תוצר ערכי ההתנגדות והקיבול (RC) מגדירים את קבוע הזמן של המעגל, המעיד על המהירות בה הקבל מטען.
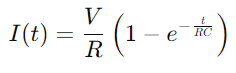 , איפה שאני הנוכחי, V הוא המתח, ר ' היא ההתנגדות, ג הוא הקיבול, t זה הזמן, ו ה הוא בסיס הלוגריתם הטבעי.נוסחה זו משקפת כיצד הזרם משתנה לאורך זמן כאשר הקבל מטען, כאשר תוצר ערכי ההתנגדות והקיבול (RC) מגדירים את קבוע הזמן של המעגל, המעיד על המהירות בה הקבל מטען.
, איפה שאני הנוכחי, V הוא המתח, ר ' היא ההתנגדות, ג הוא הקיבול, t זה הזמן, ו ה הוא בסיס הלוגריתם הטבעי.נוסחה זו משקפת כיצד הזרם משתנה לאורך זמן כאשר הקבל מטען, כאשר תוצר ערכי ההתנגדות והקיבול (RC) מגדירים את קבוע הזמן של המעגל, המעיד על המהירות בה הקבל מטען.
איור 2: מעגל סדרת RC
השחרור מתרחש עם פתיחת המתג, והופך את התהליך: האנרגיה המאוחסנת בקיבול משתחררת, וגורמת לזרם הזרם בכיוון ההפוך עד לנקז הקבל.מחזור טעינה ופריקה זה הוא קריטי ביישומים כמו המרת אות, סינון ומעגלי תזמון בגלל האופן הצפוי בו משתנים הזרם והמתח.

איור 3: קצרי סדרת RC
התנהגות מעגל הסדרה RC משתנה גם היא עם התדר.בתדרים נמוכים, הקבל פועל יותר כמו מעגל פתוח, ומכריע מאוד את זרימת הזרם.ככל שהתדר גדל, התגובה הקיבולית פוחתת, מה שמקל על הזרם לעבור.שינוי עכבה זה עם התדר מאפשר למעגל סדרת RC לפעול כמסנן, ומכריע באופן סלקטיבי תדרים מתחת לסף מסוים (תדר מפנה 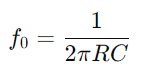 ).
).
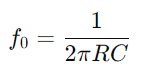 ).
).
איור 4: טעינה ופריקה של מעגלי סדרות RC
בנוסף לפעולות במצב יציב, מעגלי RC נלמדים גם לתגובותיהם החולפות כאשר הם נתונים לשינויים פתאומיים במתח, למשל כאשר מופעלים או כבוי של אספקת חשמל של DC.תרחיש זה מכונה תהליך חולף, בו המעגל עובר ממצב יציב למצב אחר.הדינמיקה של תהליך זה תלויה באופן משמעותי בקבוע הזמן של ה- RC, השולט באיזו מהירות המעגל מגיב לשינויים.
בסופו של דבר, מעגלי סדרת RC משרתים פונקציות מרובות ביישומי DC ו- AC, ומטפלים במשימות החל מעיכוב אותות לשילוב או חיבור אלמנטים שונים במעגל.צדדיות זו נובעת מהאינטראקציות הייחודיות בין הנגד לקבל, אשר יחד קובעות את התגובה הכוללת של המעגל לשינויים במתח ובתדר.

איור 5: תרשים מעגלי סדרת RC ונוסחת תדרים
במעגל סדרת RC, יחסי הגומלין בין הנגד (R) והקבל (ג) משפיע הן על זרימת הזרם והן על חלוקת המתח.התפקיד העיקרי של הנגד הוא לווסת את הזרימה הנוכחית.מערכת יחסים זו מכמתת על פי החוק של אוהם, הקובע 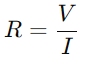 , איפה V הוא מתח ו אֲנִי הוא עדכני.בעיקרו של דבר, הנגד פועל כצוואר בקבוק, ושולט בכמה חשמל יכול לעבור בכל זמן נתון.
, איפה V הוא מתח ו אֲנִי הוא עדכני.בעיקרו של דבר, הנגד פועל כצוואר בקבוק, ושולט בכמה חשמל יכול לעבור בכל זמן נתון.
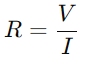 , איפה V הוא מתח ו אֲנִי הוא עדכני.בעיקרו של דבר, הנגד פועל כצוואר בקבוק, ושולט בכמה חשמל יכול לעבור בכל זמן נתון.
, איפה V הוא מתח ו אֲנִי הוא עדכני.בעיקרו של דבר, הנגד פועל כצוואר בקבוק, ושולט בכמה חשמל יכול לעבור בכל זמן נתון.פונקציית הקבל מורכבת מעט יותר מכיוון שהיא מאחסנת באופן זמני אנרגיה חשמלית ואז משחררת אותה חזרה למעגל.המתח על הקבל (VC) מתאם עם המטען המאוחסן שלו (ש) ומחושב באמצעות הנוסחה  וקשר זה מדגיש את יכולתו של הקבל להחזיק את המטען, ומשפיע ישירות על המתח שהוא מציג.במהלך הפעולה הדינמיקה של טעינה ושחרור הקבל חיוניים להבנת מעגלי RC.הקבוע הזמן (τ), מוגדר כ
וקשר זה מדגיש את יכולתו של הקבל להחזיק את המטען, ומשפיע ישירות על המתח שהוא מציג.במהלך הפעולה הדינמיקה של טעינה ושחרור הקבל חיוניים להבנת מעגלי RC.הקבוע הזמן (τ), מוגדר כ 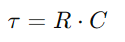 , מודד כמה מהר הקבל מגיע לכ- 63.2% מהמתח המלא המסופק על ידי המקור (V0).קבוע הזמן הזה מעיד על האופן בו המעגל מסתגל לשינויי קלט, כאשר המאפיינים של הנגד והקבלים מכתיבים את קצב ההתאמות הללו.
, מודד כמה מהר הקבל מגיע לכ- 63.2% מהמתח המלא המסופק על ידי המקור (V0).קבוע הזמן הזה מעיד על האופן בו המעגל מסתגל לשינויי קלט, כאשר המאפיינים של הנגד והקבלים מכתיבים את קצב ההתאמות הללו.
 וקשר זה מדגיש את יכולתו של הקבל להחזיק את המטען, ומשפיע ישירות על המתח שהוא מציג.במהלך הפעולה הדינמיקה של טעינה ושחרור הקבל חיוניים להבנת מעגלי RC.הקבוע הזמן (τ), מוגדר כ
וקשר זה מדגיש את יכולתו של הקבל להחזיק את המטען, ומשפיע ישירות על המתח שהוא מציג.במהלך הפעולה הדינמיקה של טעינה ושחרור הקבל חיוניים להבנת מעגלי RC.הקבוע הזמן (τ), מוגדר כ 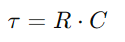 , מודד כמה מהר הקבל מגיע לכ- 63.2% מהמתח המלא המסופק על ידי המקור (V0).קבוע הזמן הזה מעיד על האופן בו המעגל מסתגל לשינויי קלט, כאשר המאפיינים של הנגד והקבלים מכתיבים את קצב ההתאמות הללו.
, מודד כמה מהר הקבל מגיע לכ- 63.2% מהמתח המלא המסופק על ידי המקור (V0).קבוע הזמן הזה מעיד על האופן בו המעגל מסתגל לשינויי קלט, כאשר המאפיינים של הנגד והקבלים מכתיבים את קצב ההתאמות הללו.המתח על הקבל בכל רגע נתון במהלך המטען ניתן על ידי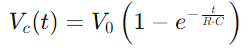 , ממחיש עלייה לא לינארית כאשר הקבל ממלא.משוואה זו מתארת כיצד קצב המטען מאט כאשר הקבל מתקרב לקיבולת המלאה.
, ממחיש עלייה לא לינארית כאשר הקבל ממלא.משוואה זו מתארת כיצד קצב המטען מאט כאשר הקבל מתקרב לקיבולת המלאה.
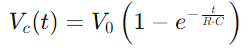 , ממחיש עלייה לא לינארית כאשר הקבל ממלא.משוואה זו מתארת כיצד קצב המטען מאט כאשר הקבל מתקרב לקיבולת המלאה.
, ממחיש עלייה לא לינארית כאשר הקבל ממלא.משוואה זו מתארת כיצד קצב המטען מאט כאשר הקבל מתקרב לקיבולת המלאה.לעומת זאת, במהלך השחרור, מתח הקבל יורד על פי 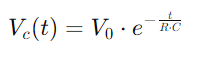 , מציג ירידה ליניארית באנרגיה המאוחסנת לאורך זמן.תהליך זה מספק תמונה ברורה של אופן שחרור האנרגיה מהקול בחזרה למעגל.ביישומי AC, הפרש הפאזה בין המתח לזרם, φ, הופך להיות קריטי.ההבדל הזה, המחושב כ
, מציג ירידה ליניארית באנרגיה המאוחסנת לאורך זמן.תהליך זה מספק תמונה ברורה של אופן שחרור האנרגיה מהקול בחזרה למעגל.ביישומי AC, הפרש הפאזה בין המתח לזרם, φ, הופך להיות קריטי.ההבדל הזה, המחושב כ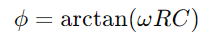 אֵיפֹה Ω מייצג תדר זוויתי, מראה את העיכוב הנגרם על ידי הקבל, המשפיע על העיתוי בין זרימת הזרם לשינויי מתח על פני הרכיבים.
אֵיפֹה Ω מייצג תדר זוויתי, מראה את העיכוב הנגרם על ידי הקבל, המשפיע על העיתוי בין זרימת הזרם לשינויי מתח על פני הרכיבים.
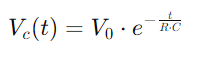 , מציג ירידה ליניארית באנרגיה המאוחסנת לאורך זמן.תהליך זה מספק תמונה ברורה של אופן שחרור האנרגיה מהקול בחזרה למעגל.ביישומי AC, הפרש הפאזה בין המתח לזרם, φ, הופך להיות קריטי.ההבדל הזה, המחושב כ
, מציג ירידה ליניארית באנרגיה המאוחסנת לאורך זמן.תהליך זה מספק תמונה ברורה של אופן שחרור האנרגיה מהקול בחזרה למעגל.ביישומי AC, הפרש הפאזה בין המתח לזרם, φ, הופך להיות קריטי.ההבדל הזה, המחושב כ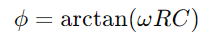 אֵיפֹה Ω מייצג תדר זוויתי, מראה את העיכוב הנגרם על ידי הקבל, המשפיע על העיתוי בין זרימת הזרם לשינויי מתח על פני הרכיבים.
אֵיפֹה Ω מייצג תדר זוויתי, מראה את העיכוב הנגרם על ידי הקבל, המשפיע על העיתוי בין זרימת הזרם לשינויי מתח על פני הרכיבים.בסך הכל, הנגד מגביל ומכוון את זרימת הזרם ואילו הקבל מאחסן ומווסת את המתח.יחד הם קובעים את מאפייני התגובה של המעגל, כגון כמה מהר הוא יכול להטעין ולפרוק ואת משמרות הפאזה המתרחשות בתרחישים זרם לסירוגין.התנהגות משולבת זו מבססת את הפעולות הבסיסיות של מעגלי סדרת RC, מה שהופך אותם לאינטגרליים ביישומים אלקטרוניים שונים.
משוואות בסיסיות של מעגל סדרות RC
כדי להבין את התנהגותו של מעגל סדרת RC, חשוב להתחיל עם המשוואות הבסיסיות המתארות את תגובתה לשינויים במתח הקלט.נניח שיש לנו מתח כניסה משתנה המיוצג כ- Vin (t), כאשר המתח על פני הנגד מתויג כ Vr (t) ובכל הקבל כ VC (t)ובמעגל סדרה, אותו זרם, זֶה) זורם דרך הנגד וגם הקבל.
החלת חוק המתח של קירצ'וף (KVL), הקובע כי המתח הכולל סביב כל לולאה סגורה במעגל חייב להיות שווה לאפס, אנו מגלים כי מתח הכניסה שווה לסכום המתחים על פני הנגד והקבל:

ניתן לחשב את המתח על פני הנגד באמצעות חוק אוהם:
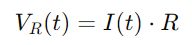
עבור הקבל, VC (T) המתח קשור למטען Q (t) הוא מחזיק, ניתן על ידי:
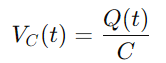
מכיוון שהזרם מוגדר כקצב זרימת המטען, יש לנו:
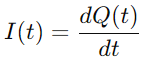
על ידי החלפה ש (t) במשוואה עבור VC (t), ושימוש בנגזרת הטעינה זֶה), אנו שואבים את משוואת ההפרש הליבה עבור מעגל סדרת RC:

החלפה נוספת ש (t) עם האינטגרל של זֶה), אנחנו מקבלים:
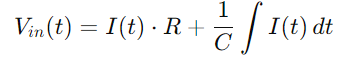
עבור ה- I (T) הנוכחי, בהתחשב בשיעור שינוי המתח על הקבל, אנו משתמשים:

שילוב כל מערכות היחסים הללו מעניק לנו את המשוואה ההפרש המתארת את המתח על הקבל:
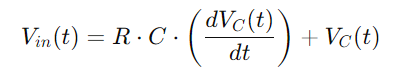
זוהי משוואה דיפרנציאלית ליניארית מסדר ראשון הלוכדת את שינוי המתח התלוי בזמן על הקבל.פתרון משוואה זו מאפשר לנו לתאר במדויק כיצד מתפתח מתח הקבל.הבנה זו היא בסיסית לניתוח מחזורי הטעינה והפריקה של הקבל, כמו גם תגובת המעגל לתדרים שונים.גישה מקיפה זו מספקת תובנה עמוקה לגבי המאפיינים הדינמיים של מעגל סדרת RC.

איור 6: משוואת דיפרנציאל מתח
עכבה של מעגל סדרות RC
כדי לשכתב את התיאור של מעגל סדרת RC, תוך התמקדות באינטראקציה אנושית והסבר ישיר ופשוט, בואו נשפר את החוויות המוחשיות ואת הפעולות שלב אחר שלב המעורבות תוך שמירה על מסר הליבה וקוהרנטיות:
במעגל סדרת RC, הנגד והקבל פועלים במקביל לשליטה על זרימת החשמל, מכריעה בעת התמודדות עם זרמים מתחלפים.העכבה המוחלטת של המעגל, המיוצגת כ- 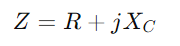 , משלב את ההתנגדות R ואת התגובה הקיבולית XC.מאפיין המפתח בהגדרה זו הוא שערכי העכבה לשני הרכיבים משתנים עם שינויי תדר.ככל שהתדירות עולה, עכבה של הקבל פוחתת, ומאפשרת ליותר זרם לעבור, ואילו ההתנגדות למעשה נשארת קבועה.
, משלב את ההתנגדות R ואת התגובה הקיבולית XC.מאפיין המפתח בהגדרה זו הוא שערכי העכבה לשני הרכיבים משתנים עם שינויי תדר.ככל שהתדירות עולה, עכבה של הקבל פוחתת, ומאפשרת ליותר זרם לעבור, ואילו ההתנגדות למעשה נשארת קבועה.
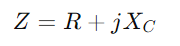 , משלב את ההתנגדות R ואת התגובה הקיבולית XC.מאפיין המפתח בהגדרה זו הוא שערכי העכבה לשני הרכיבים משתנים עם שינויי תדר.ככל שהתדירות עולה, עכבה של הקבל פוחתת, ומאפשרת ליותר זרם לעבור, ואילו ההתנגדות למעשה נשארת קבועה.
, משלב את ההתנגדות R ואת התגובה הקיבולית XC.מאפיין המפתח בהגדרה זו הוא שערכי העכבה לשני הרכיבים משתנים עם שינויי תדר.ככל שהתדירות עולה, עכבה של הקבל פוחתת, ומאפשרת ליותר זרם לעבור, ואילו ההתנגדות למעשה נשארת קבועה.העכבה, המכונה AS Z ונמדד באוהם (Ω), ממלא תפקיד קריטי בקביעת האופן בו המעגל מגיב לזרם מתחלף.כמו במעגלי סדרות RL, ההתנגדות ר ' ותגובה קיבולית xג של מעגל RC יוצר משולש המכונה משולש העכבה.משולש זה מתייחס מקרוב למשולש המתח, ועל ידי יישום המשפט הפיתגורני, אתה יכול לחשב את העכבה הכוללת של המעגל.

איור 7: נוסחת חישוב מעגלי סדרת RC
כשמדובר ביישומים מעשיים, שקול אוזניות, המשתמשות בעקרונות אלה.בדרך כלל משתמשים באוזניות בעלות עכבה גבוהה, לרוב העולות על 200 אוהם, במחשבים שולחניים, מגברי כוח וציוד שמע מקצועי.דגמי עכבה גבוהה אלה תואמים היטב את יכולות הפלט של אלקטרוניקה בדרגה מקצועית.בעת שימוש באוזניות אלה, חשוב להתאים את עוצמת הקול בהדרגה כדי למנוע עומס יתר ופגיעה ברכיבים הפנימיים העדינים, כמו סליל הקול.
לעומת זאת, אוזניות בעלות עכבה נמוכה, בדרך כלל מתחת ל 50 אוהם, עדיפות על מכשירים ניידים כמו נגני CD, נגני MD או נגני MP3.אוזניות אלה דורשות פחות כוח כדי לספק שמע באיכות גבוהה, מה שהופך אותן לאידיאליות לשימוש נייד.עם זאת, הם גם מחייבים תשומת לב מדוקדקת לרמות הרגישות כדי להבטיח ביצועים מיטביים ולמנוע נזק לאוזניות או לשמיעה.

איור 8: תרשים עכבה של מעגל סדרת RC
נהלי כניסה וניתוח של מעגלי סדרות RC
אמצעי כניסה באיזו קלות מעגל סדרת RC יכול לערוך חשמל, המחושב כהיפוך עכבה (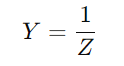 ).ערך זה משלב הן את ההתנגדות (ר ') והתגובה (X) של המעגל.ההתנגדות מתנגדת לזרימת הזרם על ידי המרת אנרגיה חשמלית לחום, ואילו תגובתו מאחסנת אנרגיה באופן זמני במעגל.
).ערך זה משלב הן את ההתנגדות (ר ') והתגובה (X) של המעגל.ההתנגדות מתנגדת לזרימת הזרם על ידי המרת אנרגיה חשמלית לחום, ואילו תגובתו מאחסנת אנרגיה באופן זמני במעגל.
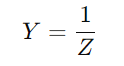 ).ערך זה משלב הן את ההתנגדות (ר ') והתגובה (X) של המעגל.ההתנגדות מתנגדת לזרימת הזרם על ידי המרת אנרגיה חשמלית לחום, ואילו תגובתו מאחסנת אנרגיה באופן זמני במעגל.
).ערך זה משלב הן את ההתנגדות (ר ') והתגובה (X) של המעגל.ההתנגדות מתנגדת לזרימת הזרם על ידי המרת אנרגיה חשמלית לחום, ואילו תגובתו מאחסנת אנרגיה באופן זמני במעגל.לחשב כניסה
התחל בכתיבת העכבה 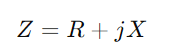 , שם R מייצג התנגדות, X לתגובה, ו י היא היחידה הדמיונית.השתמש בפורמולה y = 1/(ר ' + JX).פעולה זו כוללת מספרים מורכבים ונותנת לנו
, שם R מייצג התנגדות, X לתגובה, ו י היא היחידה הדמיונית.השתמש בפורמולה y = 1/(ר ' + JX).פעולה זו כוללת מספרים מורכבים ונותנת לנו 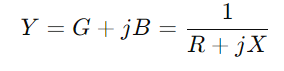 וכָּאן, ז היא המוליכות (יכולת זרימת זרם בפועל) ו ב הוא הרגישות (יכולתו של המעגל להגיב לשינויים בזרם).
וכָּאן, ז היא המוליכות (יכולת זרימת זרם בפועל) ו ב הוא הרגישות (יכולתו של המעגל להגיב לשינויים בזרם).
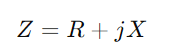 , שם R מייצג התנגדות, X לתגובה, ו י היא היחידה הדמיונית.השתמש בפורמולה y = 1/(ר ' + JX).פעולה זו כוללת מספרים מורכבים ונותנת לנו
, שם R מייצג התנגדות, X לתגובה, ו י היא היחידה הדמיונית.השתמש בפורמולה y = 1/(ר ' + JX).פעולה זו כוללת מספרים מורכבים ונותנת לנו 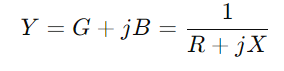 וכָּאן, ז היא המוליכות (יכולת זרימת זרם בפועל) ו ב הוא הרגישות (יכולתו של המעגל להגיב לשינויים בזרם).
וכָּאן, ז היא המוליכות (יכולת זרימת זרם בפועל) ו ב הוא הרגישות (יכולתו של המעגל להגיב לשינויים בזרם).
איור 9: מחשבון עכבה של מעגל RC סדרה
חישוב זה מגלה לא רק את המוליכות של המעגל אלא גם את מאפייני התגובה הדינמיים שלו, מכריעים לניתוח מעגלי AC.מוליכות ורגישות, שנלקחו יחד, מציינים כיצד המעגל מעביר זרם וכיצד הוא מאחסן ומשחרר אנרגיה.

איור 10: נוסחת זווית שלב
יישום מעשי
מהנדסים משתמשים בערכי כניסה כדי לשפר את תכנון המעגלים, במיוחד ביישומים בתדר גבוה כמו מעגלי תדר רדיו.התאמת כניסה מסייעת בהתאמת עכבה, הפחתת השתקפות האות והגברת יעילות ההעברה.
על ידי לימוד תגובת הכניסה, מהנדסים יכולים להעריך ולחזות את ביצועי המעגל בתנאים שונים כמו תגובת תדר, יציבות ורגישות.צייד באוסילוסקופ ובמחולל אותות כדי למדוד את המתח והזרם של המעגל בתדרים משתנים.התמקדו במיוחד בתדירות הניתוק לבדיקת תחזיות תיאורטיות ולאמתן כנגד תצפיות מעשיות.עבור מעגלי AC, התחל בקביעת התגובה (XC) של הקבל עם 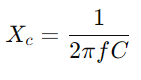 , איפה ג הוא תדר האות.חישוב העכבה המוחלטת
, איפה ג הוא תדר האות.חישוב העכבה המוחלטת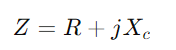 ואז כניסה
ואז כניסה 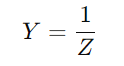 ו
ו
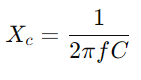 , איפה ג הוא תדר האות.חישוב העכבה המוחלטת
, איפה ג הוא תדר האות.חישוב העכבה המוחלטת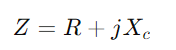 ואז כניסה
ואז כניסה 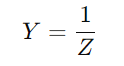 ו
ולנתח את ההבדל שלב באמצעות 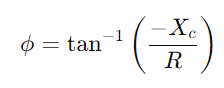 כדי להבין את שינוי צורת האות.בדוק כיצד המעגל מטפל בתדרים שונים, ובמיוחד מציין את ההתנהגות בתדר הניתוק
כדי להבין את שינוי צורת האות.בדוק כיצד המעגל מטפל בתדרים שונים, ובמיוחד מציין את ההתנהגות בתדר הניתוק 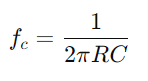 , שם המעגל עובר מעבר לחסימה לאותות.הערכת כיצד עכבה והבדל שלב משתנים בתדירות, היא קריטית לתכנון פילטרים ומעבדי אות יעילים.דונו במידת סלקטיביות התדרים, משמרות שלב והנחת האותות בגלל תכונות המעגל משפיעות על יישומים מעשיים כמו סינון וכוונון אלקטרוני.
, שם המעגל עובר מעבר לחסימה לאותות.הערכת כיצד עכבה והבדל שלב משתנים בתדירות, היא קריטית לתכנון פילטרים ומעבדי אות יעילים.דונו במידת סלקטיביות התדרים, משמרות שלב והנחת האותות בגלל תכונות המעגל משפיעות על יישומים מעשיים כמו סינון וכוונון אלקטרוני.
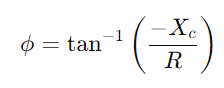 כדי להבין את שינוי צורת האות.בדוק כיצד המעגל מטפל בתדרים שונים, ובמיוחד מציין את ההתנהגות בתדר הניתוק
כדי להבין את שינוי צורת האות.בדוק כיצד המעגל מטפל בתדרים שונים, ובמיוחד מציין את ההתנהגות בתדר הניתוק 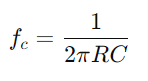 , שם המעגל עובר מעבר לחסימה לאותות.הערכת כיצד עכבה והבדל שלב משתנים בתדירות, היא קריטית לתכנון פילטרים ומעבדי אות יעילים.דונו במידת סלקטיביות התדרים, משמרות שלב והנחת האותות בגלל תכונות המעגל משפיעות על יישומים מעשיים כמו סינון וכוונון אלקטרוני.
, שם המעגל עובר מעבר לחסימה לאותות.הערכת כיצד עכבה והבדל שלב משתנים בתדירות, היא קריטית לתכנון פילטרים ומעבדי אות יעילים.דונו במידת סלקטיביות התדרים, משמרות שלב והנחת האותות בגלל תכונות המעגל משפיעות על יישומים מעשיים כמו סינון וכוונון אלקטרוני.גישה זו מפרקת את התהליכים התפעוליים לצעדים הניתנים לניהול, ומעשירה את הבנת המשתמש בתובנות מעשיות לגבי טיפול וניתוח מעגלי סדרות RC.

איור 11: מאפיינים של מעגלי סדרות RC
תרשים פסור של מעגל סדרת RC
במעגל סדרת RC, כל האלמנטים חולקים את אותו הזרם בגלל תצורת הסדרה שלהם.זרם אחיד זה משמש כבסיס לתרשים הפסור שלנו, המסייע בהמחיש הקשר בין מתחים שונים לזרמים שונים במעגל.בואו נקבע את הנוכחי הזה אֲנִי כפאסור ההתייחסות, הממוקם באפס מעלות בתרשים.בתרשים, הזרם אֲנִי מוגדר אופקית ימינה, מקים את קו ההתייחסות לתואר אפס.המתח על פני הנגד (Uר ') נמצא בשלב עם הזרם מכיוון שנגדים אינם גורמים לשינוי שלב.כָּך, Uר ' נמשך כווקטור אופקי באותו כיוון כמו אֲנִי, משתרע מהמקור.

איור 12: דיאגרמת פאסור מעגלי סדרת RC
לעומת זאת, המתח על הקבל (Uג) מוביל את הזרם ב 90 מעלות בגלל המאפיין הקיבולי של עיכוב השלב הנוכחי.מתח זה מיוצג על ידי וקטור אנכי המפנה כלפי מעלה, החל מקצה הקצה Uר ' וֶקטוֹר.המתח הכולל U במעגל הוא הסכום הווקטורי של U ראנד Uגוסכום זה מהווה משולש נכון עם Uר ' וכן Uג כצדדים הסמוכים והפוכים, בהתאמה.ההיפוטוזה של המשולש הזה, המשתרעת מהמקור לקצה של Uג וקטור, מייצג Uו
הזרם הסינוסואידי דרך המעגל ניתן על ידי חטא (ωt), כאשר IM הוא משרעת הזרם המרבית ו Ω הוא התדר הזוויתי.כתוצאה מכך, המתח על פני הנגד הוא 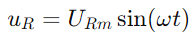 , שיקוף את צורת הגל הנוכחית.המתח על הקבל ניתן על ידי
, שיקוף את צורת הגל הנוכחית.המתח על הקבל ניתן על ידי 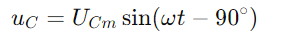 , מציין שינוי שלב של -90 ° (או 90 מעלות לפני הזרם).המשולש הימני של תרשים הפסור מבהיר את זה
, מציין שינוי שלב של -90 ° (או 90 מעלות לפני הזרם).המשולש הימני של תרשים הפסור מבהיר את זה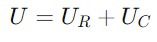 הוא לא רק בעוצמה אלא גם בקשר שלב, עם וקטור המתח הסופי ((U) השלמת המשולש.
הוא לא רק בעוצמה אלא גם בקשר שלב, עם וקטור המתח הסופי ((U) השלמת המשולש.
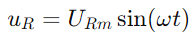 , שיקוף את צורת הגל הנוכחית.המתח על הקבל ניתן על ידי
, שיקוף את צורת הגל הנוכחית.המתח על הקבל ניתן על ידי 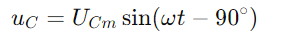 , מציין שינוי שלב של -90 ° (או 90 מעלות לפני הזרם).המשולש הימני של תרשים הפסור מבהיר את זה
, מציין שינוי שלב של -90 ° (או 90 מעלות לפני הזרם).המשולש הימני של תרשים הפסור מבהיר את זה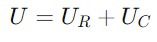 הוא לא רק בעוצמה אלא גם בקשר שלב, עם וקטור המתח הסופי ((U) השלמת המשולש.
הוא לא רק בעוצמה אלא גם בקשר שלב, עם וקטור המתח הסופי ((U) השלמת המשולש.
איור 13: תרשים פסור מתח של מעגל סדרת RC
נקודות מפתח בניתוח מעגלי RC סדרות
עכבה במעגל RC של סדרה, המיוצגת כ- Z, משלב התנגדות (ר ') וההשפעה המגיבה של הקיבול למדד יחיד המשתנה עם תדר האות.זה בא לידי ביטוי באופן מתמטי 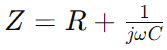 , איפה Ω הוא התדר הזוויתי ו ג הוא הקיבול.כָּאן, ר ' מהווה את החלק האמיתי של העכבה, ו
, איפה Ω הוא התדר הזוויתי ו ג הוא הקיבול.כָּאן, ר ' מהווה את החלק האמיתי של העכבה, ו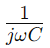 מייצג את החלק הדמיוני, ומציין כיצד הקבל משפיע על המעגל.
מייצג את החלק הדמיוני, ומציין כיצד הקבל משפיע על המעגל.
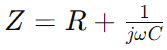 , איפה Ω הוא התדר הזוויתי ו ג הוא הקיבול.כָּאן, ר ' מהווה את החלק האמיתי של העכבה, ו
, איפה Ω הוא התדר הזוויתי ו ג הוא הקיבול.כָּאן, ר ' מהווה את החלק האמיתי של העכבה, ו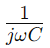 מייצג את החלק הדמיוני, ומציין כיצד הקבל משפיע על המעגל.
מייצג את החלק הדמיוני, ומציין כיצד הקבל משפיע על המעגל.האופן בו עכבה משתנה עם התדר היא מרכזית לשימוש במעגלי RC סדרות ביישומי סינון.בתדרים נמוכים יותר, המעגל מציג עכבה גבוהה יותר, וחוסם למעשה את התדרים הללו.לעומת זאת, בתדרים גבוהים יותר, העכבה יורדת, ומאפשרת לתדרים אלה לעבור בצורה חופשית יותר.התנהגות זו הופכת את מעגלי הסדרה RC לאידיאליים למשימות כמו סינון רעש לא רצוי בתדר נמוך או לעבור אותות בתדר גבוה.

איור 14: תרשים וקטור עכבה של מעגל סדרת RC
מַסְקָנָה
החל מסינון תדרים לא רצויים ועד עיצוב תגובות האות, מעגל סדרת RC מסייע במגוון רחב של פונקציות אלקטרוניות.על ידי הבנת העקרונות הבסיסיים כמו עכבה, יחסי פסור והתנהגות תלויה בתדרים של מעגלים אלה, מהנדסים ומעצבים מצוידים לפתרונות מלאכה המנהלים ביעילות את שלמות האות במערכות אלקטרוניות מורכבות.הבחינה המפורטת של מעגלים אלה, הנתמכת על ידי ניתוח מתמטי וייצוגים חזותיים כמו דיאגרמות פסור, מציעה תובנה מקיפה החשובה לכל מי שמחפש להעמיק את הבנתם בדינמיקת המעגלים האלקטרוניים או כדי לשפר את כישוריהם המעשיים בעיצוב ופתרון בעיות במעגל.
שאלות נפוצות [שאלות נפוצות]
1. מה העיקרון של מעגל RC?
העיקרון של מעגל RC (Capacitor) סובב סביב תהליכי הטעינה והפרקה של הקבל דרך הנגד.במעגל זה, יכולתו של הקבל לאחסן ולשחרר אנרגיה חשמלית מקיימת אינטראקציה עם הנגד, השולט בקצב בו הקבל מטען או משחרר.
2. מדוע מעגל RC מוביל זרם?
במעגל RC, הזרם מוביל את המתח על הקבל מכיוון שהקבל צריך להתחיל לטעון לפני שהמתח שלו יכול לעלות.מכיוון שהזרם זורם אל הקבל כדי לטעון אותו, הזרם מגיע לשיא לפני המתח על הקבל מגיע למקסימום שלו.השפעה זו גורמת לשינוי שלב בו השלב הנוכחי מוביל את שלב המתח בעד 90 מעלות, תלוי בתדירות האות הקלט.
3. כיצד משתנה המתח במעגל RC?
שינוי המתח במעגל RC במהלך הטעינה מתואר על ידי פונקציה מעריכית.כאשר מופעל מתח, המתח על הקבל עולה תחילה במהירות, אז מאט כשהוא מתקרב למתח האספקה.מבחינה מתמטית, זה בא לידי ביטוי כמו 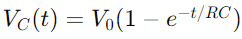 , איפה Vג(t) הוא המתח על הקבל בזמן T, V0 הוא מתח האספקה, ו- RC הוא קבוע הזמן של המעגל, וקובע כמה מהר הקבל מטען.לעומת זאת, במהלך הפריקה, המתח על הקבל יורד באופן אקספוננציאלי, בעקבות המשוואה
, איפה Vג(t) הוא המתח על הקבל בזמן T, V0 הוא מתח האספקה, ו- RC הוא קבוע הזמן של המעגל, וקובע כמה מהר הקבל מטען.לעומת זאת, במהלך הפריקה, המתח על הקבל יורד באופן אקספוננציאלי, בעקבות המשוואה  ו
ו
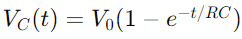 , איפה Vג(t) הוא המתח על הקבל בזמן T, V0 הוא מתח האספקה, ו- RC הוא קבוע הזמן של המעגל, וקובע כמה מהר הקבל מטען.לעומת זאת, במהלך הפריקה, המתח על הקבל יורד באופן אקספוננציאלי, בעקבות המשוואה
, איפה Vג(t) הוא המתח על הקבל בזמן T, V0 הוא מתח האספקה, ו- RC הוא קבוע הזמן של המעגל, וקובע כמה מהר הקבל מטען.לעומת זאת, במהלך הפריקה, המתח על הקבל יורד באופן אקספוננציאלי, בעקבות המשוואה  ו
ו עלינו
שביעות רצון לקוחות בכל פעם.אמון הדדי ואינטרסים משותפים.
עלינו
שביעות רצון לקוחות בכל פעם.אמון הדדי ואינטרסים משותפים.
מבחן תפקוד.המוצרים הגבוהים ביותר חסכוניים והשירות הטוב ביותר הם המחויבות הנצחית שלנו.
מאמר חם
- הם CR2032 ו- CR2016 ניתן להחלפה
- MOSFET: הגדרה, עקרון עבודה ובחירה
- התקנת ממסר ובדיקה, פרשנות של דיאגרמות חיווט ממסר
- CR2016 לעומת CR2032 מה ההבדל
- NPN לעומת PNP: מה ההבדל?
- ESP32 לעומת STM32: איזה בקר מיקרו עדיף לך?
- LM358 מגבר תפעולי כפול מדריך מקיף: Pinouts, דיאגרמות מעגלים, מקבילות, דוגמאות שימושיות
- CR2032 VS DL2032 VS CR2025 מדריך השוואה
- הבנת ההבדלים ESP32 ו- ESP32-S3 ניתוח טכני וביצועים
- ניתוח מפורט של מעגל סדרת RC
 ניתוח מעמיק של דיודות 1N4148: מצבי הפעלה, מפרטים ותרחישי שימוש
ניתוח מעמיק של דיודות 1N4148: מצבי הפעלה, מפרטים ותרחישי שימוש
2024-05-08
 הבנת הסוגים והשימושים של משאבות תזוזה דינאמיות וחיוביות
הבנת הסוגים והשימושים של משאבות תזוזה דינאמיות וחיוביות
2024-05-07
מספר חלק חם
 CL10C080CB8NCNC
CL10C080CB8NCNC GJM1555C1H1R6WB01D
GJM1555C1H1R6WB01D CGA4J3C0G2E222J125AA
CGA4J3C0G2E222J125AA UMK325BJ475MNHT
UMK325BJ475MNHT CC0603FRNPO9BN620
CC0603FRNPO9BN620 CL21F105ZAFNNNF
CL21F105ZAFNNNF LD051A300JAB4A
LD051A300JAB4A GQM1555C2D5R9BB01D
GQM1555C2D5R9BB01D 04025C681JAJ2A
04025C681JAJ2A 1210YG685ZAT2A
1210YG685ZAT2A
- GRM1556R1HR70BD01D
- TAWD336M016R0600
- VS-70TPS12PBF
- MCIMX280DVM4B
- XR16M654IV80-F
- ISL24010IVZ-T
- ISL8112IRZ
- MCR01MZPJ104
- TX1344NLT
- 1MBI400N-120-01
- DSA1508-20A
- TDC1000PWR
- VB921ZVFI
- TPA3128D2DAPR
- CD74HC4067SM96
- NX20P0407UKAZ
- TMS320C6472ECTZA6
- PSD311B-70J
- PCI2050PDV
- SM320F2812PGFMEP
- FQP6N80C
- BCM56305B1KEBG
- CY2292SXL-1J5
- CY284010XCT
- HM514256AZP-8
- MIC811TUYTR
- SST29LE512-150-4C-NH
- UCC3882PW/
- BCM3140A3IPBG
- PS161HDMLQFP64G-A0
- SED1345FOA
- SF3700-75A1SE
- SG7806AT/883B
- SDSDQ-1024
- APP5301BFCB1413-DB
- BCM7429B0KFEBA1G
- LAN91C113-NU-E2
- V300B2.2C100BL
- SN74LVC2G32DCU